Billboard与施密特正交

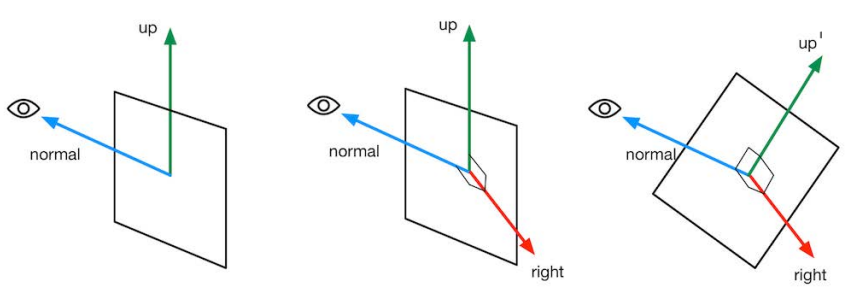
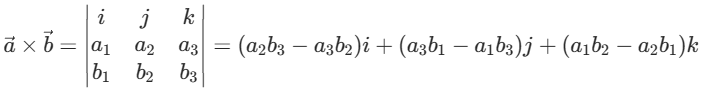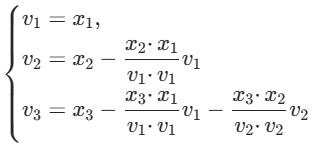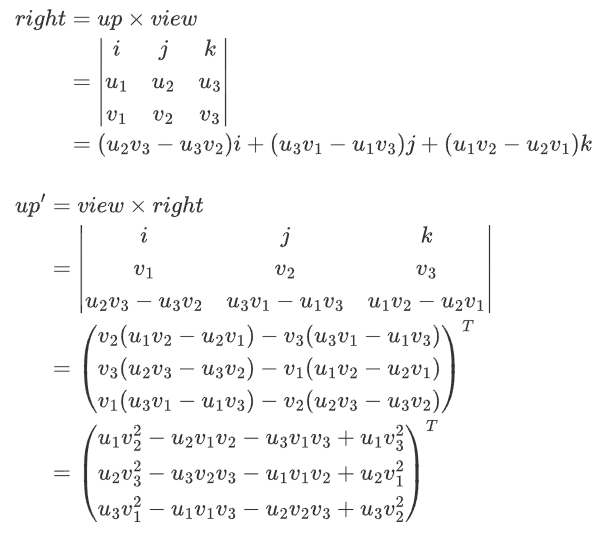在游戏开发的过程中，Billboard的一般做法是通过view和up两个向量构建一个旋转矩阵，从而调整sprite facing使其与观察空间某个向量对齐（up / normal），而众所周知构建一个旋转矩阵需要三个正交基，但我们现在就只有view和up两个基，还不正交，所以免不了要用叉乘对原来这两个二维基向量进行“升维”

具体步骤是，先用 up×view 算出 right，构建出一个临时的坐标空间；然后再以这个临时空间为参考系，用 normal×right 算出up’，再在这由两个向量张成的二维平面上再做一次升维。

因为这样得到的三个基向量可以保证相互正交，所以像这样构建旋转矩阵是非常合理的。

这是叉乘的做法。

但我们又知道，旋转矩阵之所以要用三个正交基去构建，是因为他本身就是一个标准正交矩阵，而在 $$\mathbb{R}^3$$ 找一个平面的正交基可以使用施密特正交化，那上面提到的叉乘这种做法又和施密特正交有什么关系呢？

我们不妨由公式做一些简单的推导

假设有 $$view=(v_1,v_2,v_3)$$ ， $$up=(u_1,u_2,u_3)$$

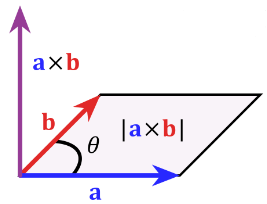
依据叉乘公式

和施密特正交化公式

叉乘法先求 right 再求 up’

而施密特正交化结果：

类似的可以求出 right，可以发现两个结果差了一个模长的平方倍，如果进行正交化的几个基均为标准基（即模长均为 1），那么这两个结果应该是一模一样的

两种方法的区别在于

1、叉乘法有先后顺序，而施密特正交化没有

2、叉乘法可以理解为升维，而施密特则可以理解为投影（本来也是这么推出来的，感兴趣可以看看下面这篇）

而从实践的角度，显然叉乘法更为直观…. 所以这篇文章只是提供了一种另类的理解方式，把两个看似无关的东西联系在了一起（就摁水）

大概就酱、