Bezier曲线缺点

Bezier曲线一旦确定了特征多边形的顶点数 $n+1$ ，也就决定了曲线的阶次（n次）。如果阶数过高，则曲线中会有大量极值点，造成曲线波动现象明显
Bezier曲线或曲面的拼接比较复杂
Bezier曲线或曲面不能作局部修改，牵一发而动全身。因为每个Bernstein多项式在整个区间 $[0,1]$ 上都有支撑，所以每个控制点对整条曲线都有影响

B样条曲线

采用分段连续多项式，整条曲线用一个完整的表达式表达，但表达式内部分量分段。使用低次曲线克服波动，使用分段多项式克服无法局部修改的局限

要求： $n+1$ 个型值点，共 $n$ 个区间，每个区间构造一个三次多项式，这 $n$ 个三次多项式拼在一起可以表达出特定的曲线，且段与段之间需要满足 $C^2$ 连续

数学表达式： $P(u)=\sum_{i=0}^nP_iB_{i,k}(u),u\in[u_{k-1},u_{n+1}]$

其中 $P_i(i=0,1,\ldots,n)$ 是控制多边形的顶点

$B_{i,k}(u)$ 称为 $k$ 阶 $k-1$ 次B样条基函数， $k$ 刻画阶数， $k\in[2,n+1]$

对于Bezier曲线，阶数 = 次数；对于B样条曲线，阶数=次数+1

B样条基函数是一个称为节点向量的非递减的参数 $u$ 的序列所决定的 $k$ 阶分段多项式，这个序列称为节点向量， $u\in [u_{k-1},u_{n+1}]$

de Boor-Cox 递推
每个 $k$ 阶 $k-1$ 次B样条基函数，都可以用低一次的两个基函数的线性组合构造
$$
B_{i,k}(u)= \frac{u-u_i}{u_{i+k-1}-u_i}B_{i,k-1}(u)+ \frac{u_{i+k}-u}{u_{i+k}-u_{i+1}}B_{i+1,k-1}(u)
$$

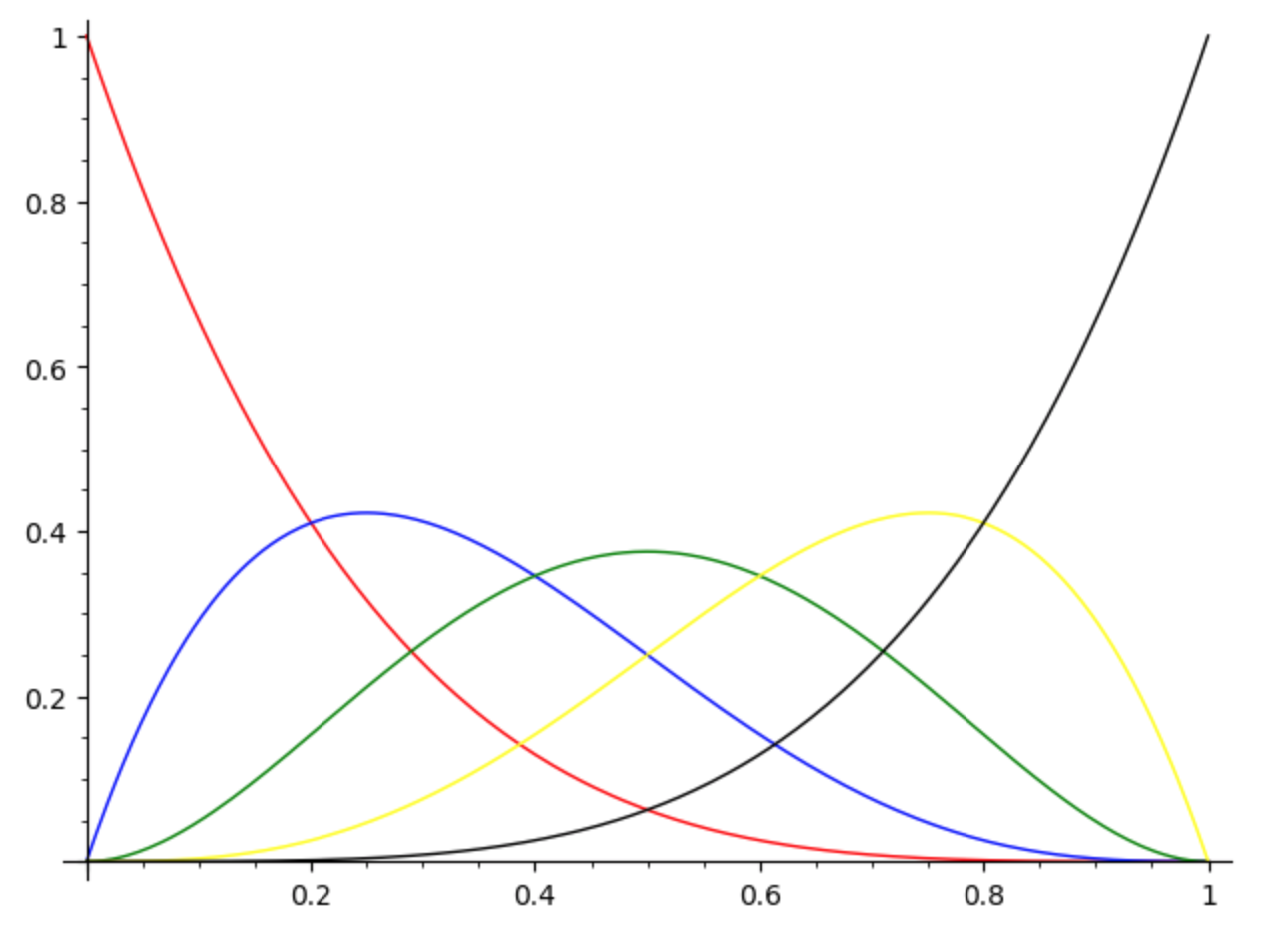
以一次到三次基函数为例，给出表达式和图像如下：

$$
\displaylines{
\begin{aligned}
B_{i,1}(u)&=
\begin{cases}
1&u_i<u<u_{i+1}\\
0&其他
\end{cases}\
\end{aligned}
}
$$

$$
\displaylines{
B_{i,2}(u)=
\begin{cases}
\dfrac{u-u_i}{u_{i+1}-u_i}&u_i\leq u\leq u_{i+1}\\
\dfrac{u_{i+2}-u}{u_{i+2}-u_{i+1}}&u_{i+1}\leq u\leq u_{i+2}\\
0&\text{其它}
\end{cases}
}
$$

$$
\displaylines{
B_{i,3}(u)=
\begin{cases}
\dfrac{u-u_{i}}{u_{i+2}-u_{i}}\cdot \dfrac{u-u_{i}}{u_{i+1}-u_{i}},&u_{i}\leq u<u_{i+1}\\
\dfrac{u-u_{i}}{u_{i+2}-u_{i}}\cdot\dfrac{u_{i+2}-u}{u_{i+2}-u_{i+1}}+\dfrac{u_{i+3}-u}{u_{i+3}-u_{i+1}}\cdot\dfrac{u-u_{i+1}}{u_{i+2}-u_{i+1}},&u_{i+1}\leq u<u_{i+2}\\
\dfrac{(u_{i+3}-u)^2}{(u_{i+3}-u_{i+1})(u_{i+3}-u_{i+2})},&u_{i+2}\leq u<u_{i+3}\\
0,&\text{其他}
\end{cases}
}
$$

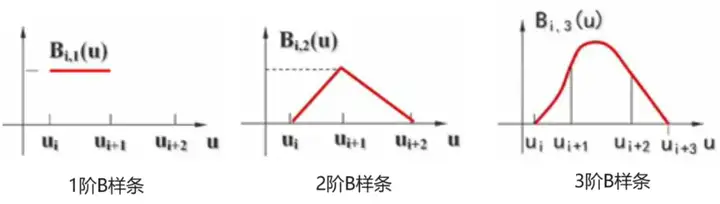
对于 $B_{i,1}$ （1阶0次基函数）来说，涉及到 $u_i$ 到 $u_{i+1}$ 一个区间，即一阶的多项式涉及1个区间2个节点； $B_{i,2}$ 由 $B_{i,1}$ 和 $B_{i+1,1}$ 组成，因此 $B_{i,2}$ 涉及2个区间3个节点；同理 $B_{i,3}$ 涉及3个区间4个节点，…， $k$ 阶 $k-1$ 次B样条基函数 $B_{i,k}(u)$ 涉及 $k$ 个区间 $k+1$ 个节点，所有基函数从 $B_{0,k}(u)$ 到 $B_{n,k}(u)$ 共涉及 $n+k+1$ 个节点（型值点个数+阶数=节点数）

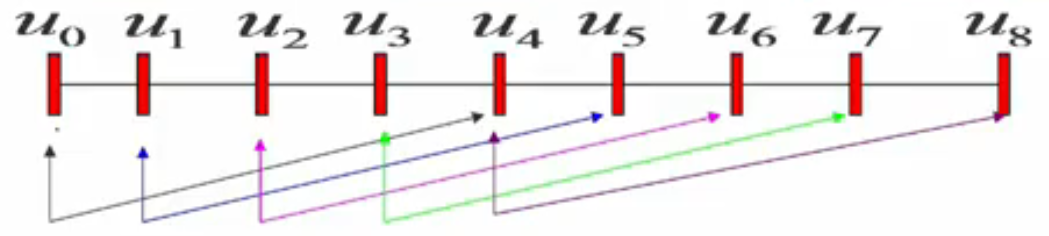
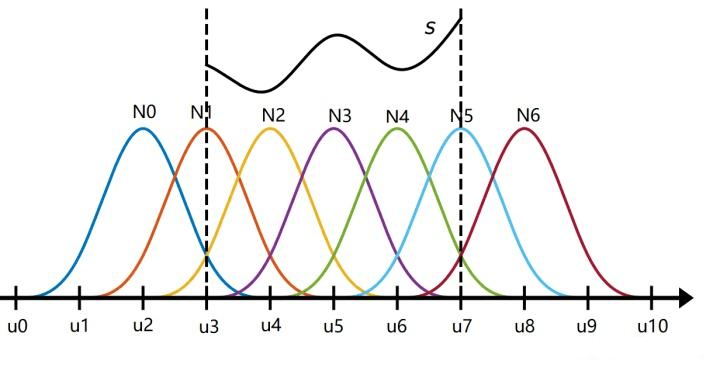
如图， $k=4$ ， $n=4$ ，每个基函数涉及 $k+1=5$ 个节点，共 $n+1=5$ 个型值点，5个基函数，5个节点向量，涉及 $n+k+1=9$ 个节点

具体来说， $B_{0,4}(u)$ 涉及 ${ u_0,u_1,u_2,u_3,u_4 }$ ， $B_{1,4}(u)$ 涉及 ${ u_1,u_2,u_3,u_4,u_5 }$ ，…， $B_{4,4}(u)$ 涉及 ${ u_4,u_5,u_6,u_7,u_8 }$ ，但区间合法的条件需要一个区间包括足够多的基函数支撑，也即有效区间是仅包括 ${ u_3,u_4,u_5 }$ 这三个节点的区间，即 $[u_3,u_4]$ 和 $[u_4,u_5]$ 两段区间，所以原曲线可由2段3次曲线构成，更一般的， $n+1$ 个型值点， $k$ 阶B样条，可由 $n-k+2$ 段 $k-1$ 次曲线段组成（控制点个数 - 阶数 + 1）

B样条基函数性质
局部支承性：
$$
\displaylines{
B_{i,k}(u)
\begin{cases}
\ge0&u\in[u_i,u_{i+k}]\\
=0&其他
\end{cases}
}
$$

而Bezier在整个区间非0。对每个区间 $(u_i,u_{i+k})$ , 至多只有 $k$ 个基函数在其上非零