一、引入

Alt text

计算机图形学下关于“实时”的定义：>30fps，<30fps称为离线

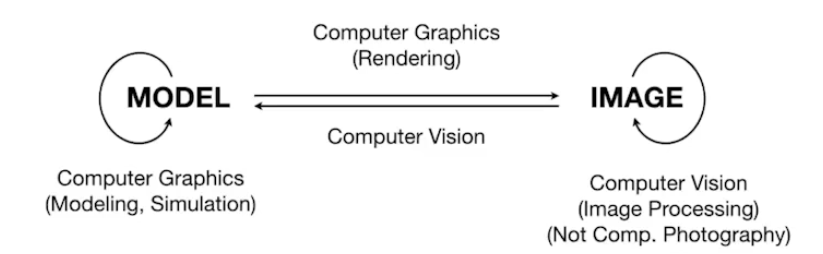
计算机视觉与计算机图形学的区别：
Alt text

二、线代基础

基础运算

叉乘基本运算
$$
\displaylines{\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}\\
\vec{a}\times\vec{a}=\vec{0} \\
\vec{a}\times(\vec{b}+\vec{c})=\vec{a}\times\vec{b}+\vec{a}\times\vec{c} \\
\vec{a}\times(k\vec{b})=k(\vec{a}\times\vec{b})}
$$

图形学叉乘应用：判断左/右&内/外

正交坐标系定义
$$
\displaylines{
||\vec{u}||=||\vec{v}||=||\vec{w}||\\
\vec{u}\cdot\vec{v}=\vec{v}\cdot\vec{w}=\vec{w}\cdot\vec{u}\\
\vec{w}=\vec{u}\times\vec{v}（右手）\\
\vec{p}=(\vec{p}\cdot\vec{u})\vec{u}+(\vec{p}\cdot\vec{v})\vec{v}+(\vec{p}\cdot\vec{w})\vec{w}}
$$

矩阵乘法
要第几行第几列，就去找第几行和第几列，左管行，右管列

设矩阵A和矩阵B，则：

1、AB和BA大多数情况下不等

2、只要不涉及前后交换，以下等式均成立
$$
\displaylines{
(AB)C=A(BC)\\
A(B+C) = AB +AC\\
(A+B)C =AC ＋BC\\
}
$$

矩阵和向量的乘法

总是把向量视作列向量并置于乘号右边

矩阵转置（ij -> ji）

$$
(AB)^T=B^TA^T
$$

单位矩阵

$$
\displaylines{
AA^{-1}=A^{-1}A=I\\
AB^{-1}=B^{-1}A^{-1}
}
$$

向量乘法的矩阵形式

$$
\displaylines{
\vec{a}\cdot\vec{b}=\vec{a}^T\vec{b}\\
\vec{a}\times\vec{b}=A^*b
}
$$

向量变换

2d

线性变换

缩放	切变

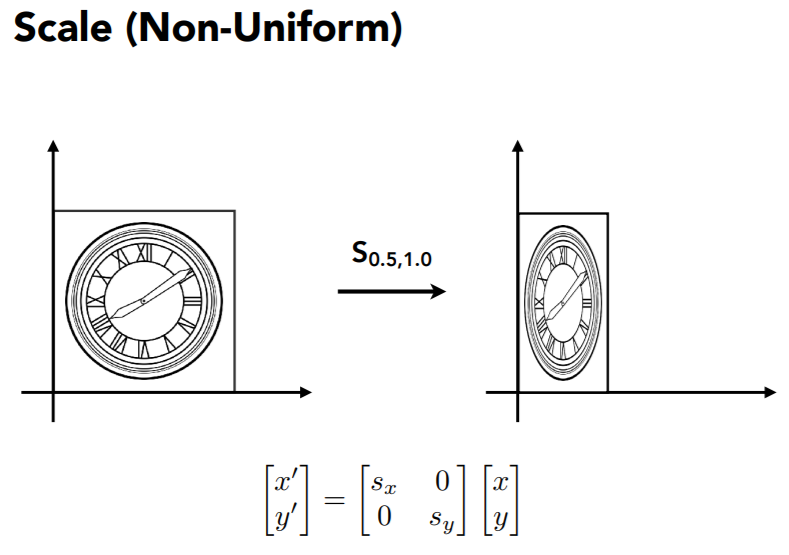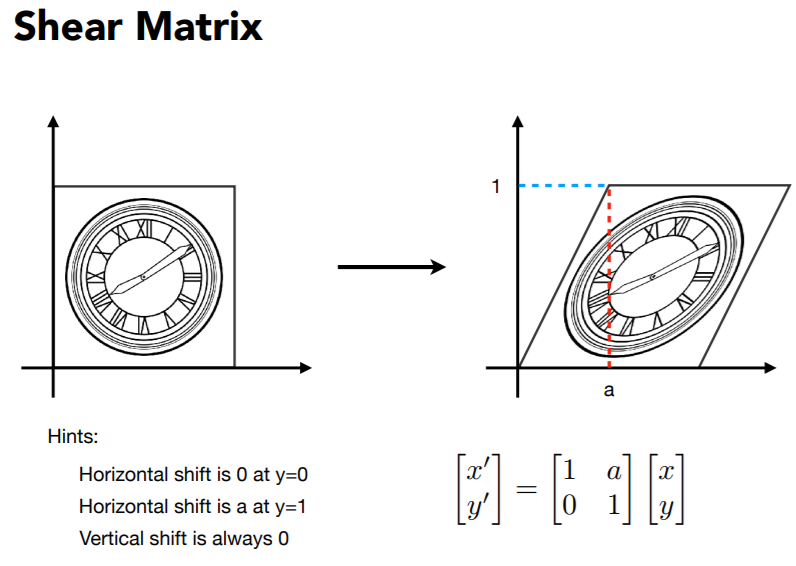对称	旋转

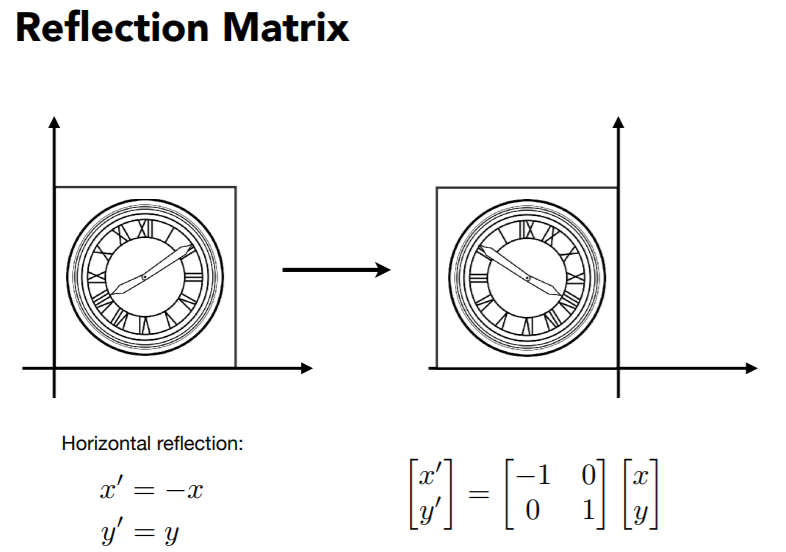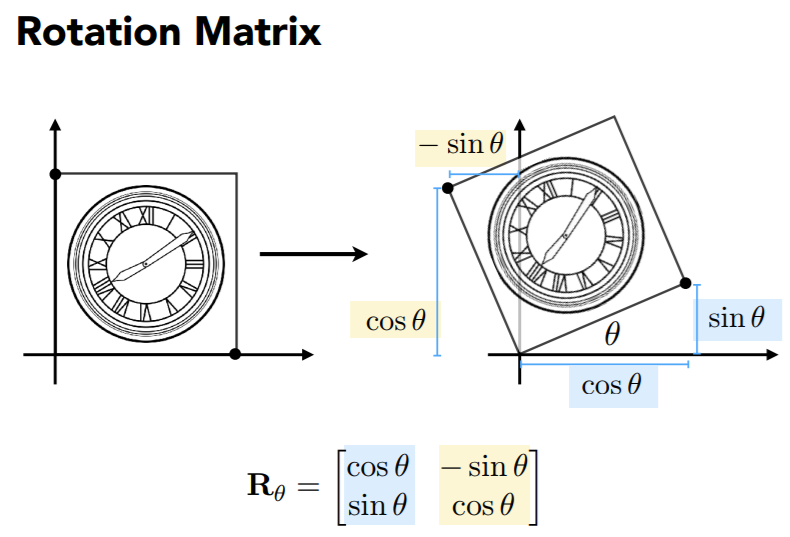相同维度线性变化：
$$
\displaylines{
x’=ax+by\\
y’=cx+dy\\
\left[
\begin{matrix}
x’\\
y’\\
\end{matrix}
\right]=
\left[
\begin{matrix}
a&b\\
c&d\\
\end{matrix}
\right]
\left[
\begin{matrix}
x\\
y\\
\end{matrix}
\right]\\
x’=Mx
}
$$

齐次坐标

点(x,y,1) 向量(x,y,0) 则有：

点-点=向量，向量$\pm$向量=向量，点+向量=点，点+点=两点的中点

在齐次坐标中，$\left(\begin{matrix}x\\ y\\ w \end{matrix} \right)$都视作$\left(\begin{matrix}x/w\\ y/w\\ 1 \end{matrix}\right)$，其中$w≠0$

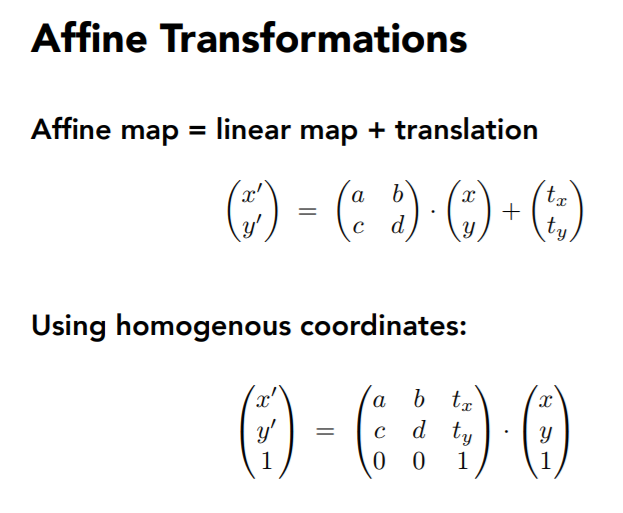
仿射变换

仿射变化=线性变换+平移

矩阵相乘不满足结合律

例如，先旋转再平移和先平移再旋转所得结果不一样

变换合成（结合律的体现）

Alt text

3d

平移	缩放

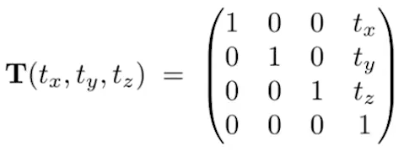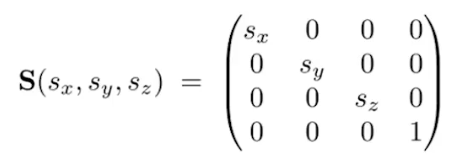旋转

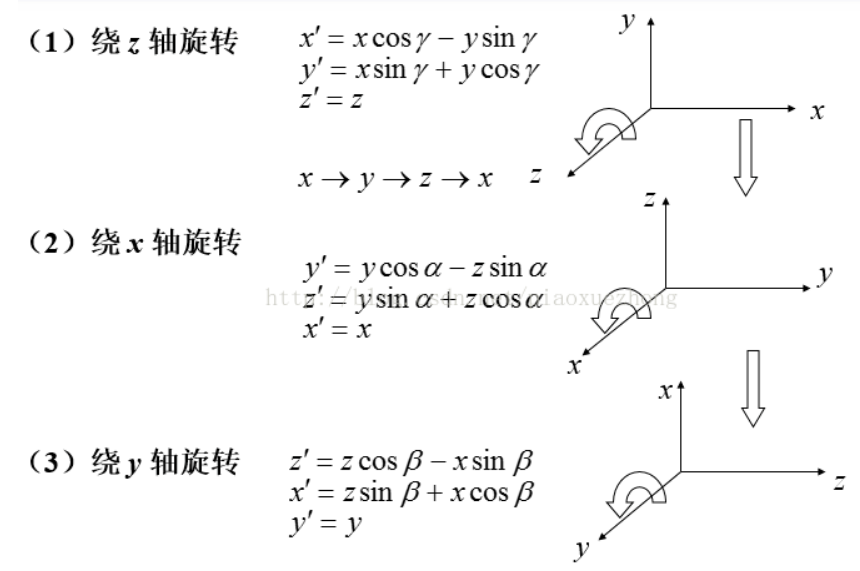3d旋转变换矩阵遵循循环对称：$X\times Y=Z,\ \ Y\times Z=X,\ \ Z\times X=Y$

合成的旋转变换：$R_{xyz}(\alpha,\beta,\gamma)=R_x(\alpha)R_y(\beta)R_z(\gamma)$

罗德里格斯旋转公式

绕旋转轴n旋转α角度
$$
R(n,\alpha)=cos(\alpha)E+(1-cos(\alpha))nn^T+sin(\alpha)
\left(\begin{matrix}
0 & -n_z & n_y \\
n_z & 0 & -n_x \\
-n_y & n_x & 0
\end{matrix}\right)
$$
推导过程：

罗德里格斯公式Rodrigues'Rotation Formula推导

四元数：旋转与旋转之间的差值，具体内容略去

视图 / 相机变换

如何将三维变成二维并在屏幕上显示出来

1、模型变换 (M) 2、相机变换 (V) 3、投影变换 (P)

定义相机属性

1、位置 $\vec{e}$

2、视线方向 $\widehat{g}$

3、垂直方向 $\widehat{t}$

初始：up at Y, look at -Z

如果把摄像机和世界一起变换，那么照片是一样的，所以把摄像机变换到新坐标系的原点，其他所有物体也做同样的变换

teg坐标系怎么转变为xyz坐标系

$M_{view}$ in Math?

$M_{view}$=$R_{view}$$T_{view}$

1、先做平移，$T_{view}=\left[\begin{matrix}1&0&0&-x_e\\ 0&1&0&-y_e\\ 0&0&1&-z_e\\ 0&0&0&1\end{matrix}\right]$

2、再做旋转，顺着思路要把 $\widehat{g}$ 旋转到$-Z$坐标轴，把 $\widehat{t}$ 旋转到$Y$坐标轴，把$（g\times t）$旋转到 $x$ 坐标轴，但这样的旋转矩阵非常难写

所以采用逆向思路，把坐标轴移到相机坐标轴，通过逆操作写（该旋转矩阵为正交矩阵，其逆矩阵就是它的转置矩阵）（基变换）

$$
R^{-1}_{view}=
\left[\begin{matrix}
x_{\widehat g\times \widehat t} & x_t & x_{-g} & 0 \\
y_{\widehat g\times \widehat t} & y_t & y_{-g} & 0 \\
z_{\widehat g\times \widehat t} & z_t & z_{-g} & 0 \\
0 & 0 & 0 & 1
\end{matrix}\right]
$$

$$
R_{view}=
\left[\begin{matrix}
x_{\widehat g\times \widehat t} & y_{\widehat g\times \widehat t} & z_{\widehat g\times \widehat t} & 0\\
x_t & y_t & z_t & 0\\
x_{-g} & y_{-g} & z_{-g} & 0\\
0 & 0 & 0 & 1
\end{matrix}\right]
$$

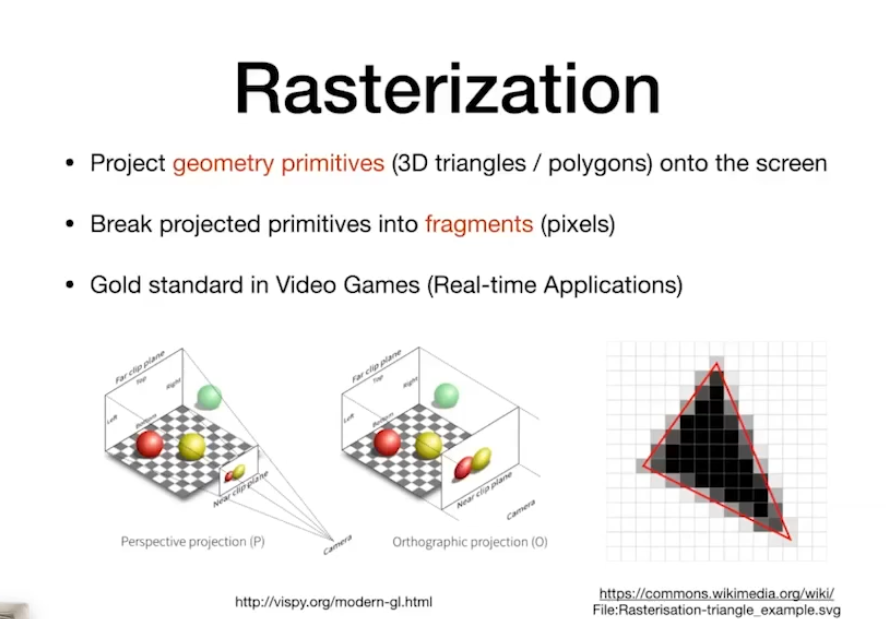
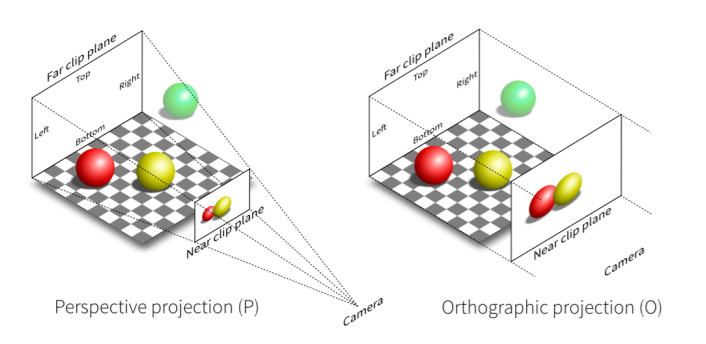
投影变换（难点）

Alt text

正交投影

相机位置无限远，没有远近概念（忽略深度信息）

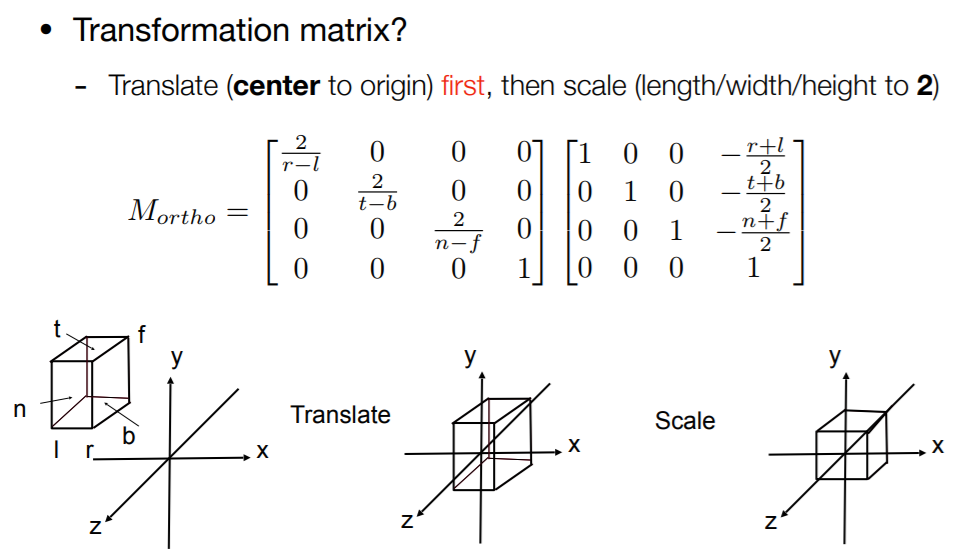
步骤：先做平移，再做缩放，目标是吧投影全塞在 $[-1,1]^2$ 的长方体内

Alt text

透视投影

用的最广泛的投影，近大远小，

根据已知的$Near、Far、Fov、Aspect$确定透视投影的投影矩阵，如下
$$
M_{frustum}=
\left[\begin{matrix}
\frac{cot\frac{FOV}{2}}{Aspect} & 0 & 0 & 0 \\
0 & cot{\frac{FOV}{2}} & 0 & 0 \\
0 & 0 & \frac{Near+Far}{Near-Far} & -\frac{2Near·Far}{Near-Far} \\
0 & 0 & 1 & 0
\end{matrix}\right]
$$
具体推导如下：
Alt text