Blinn-Phong光照模型
漫反射
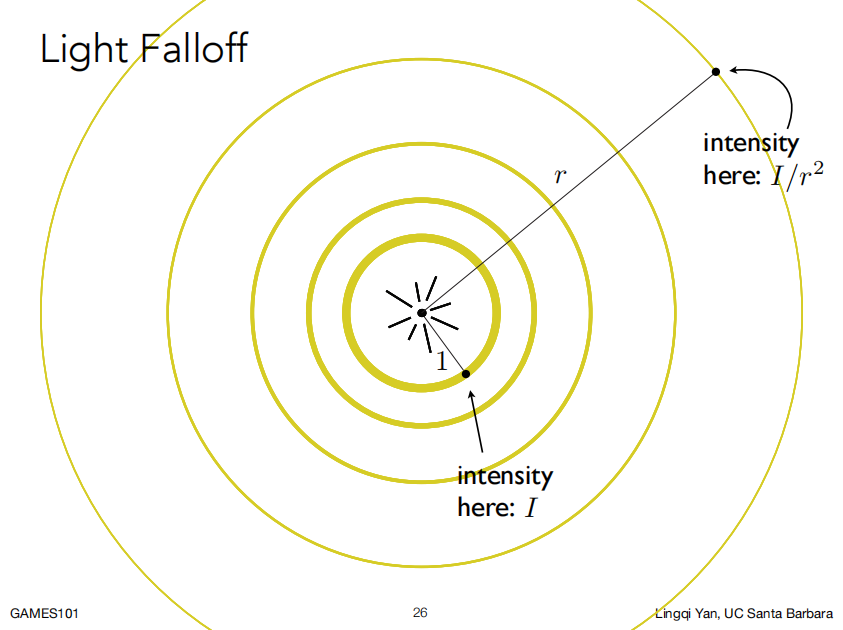
要知道物体表面多亮,就要知道从光源到物体表面发射的能量光是多少,单位的能量光在单位球上的能量表示为 I,同一个点上的能量随着光不断向外传播而逐渐减少, 根据能量守恒定律,每一个球面上的总能量都是相同的(这在之后辐射度量学会有补充)
由此可以得到关系式:
$$
1^24πI=r^24πI’
$$
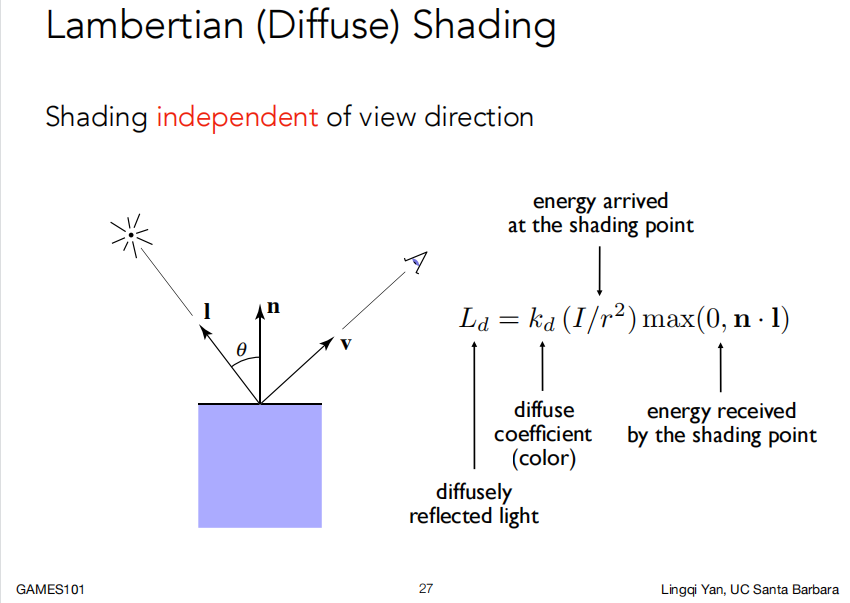
再计算物体表面着色点反射多少能量光给摄像机接收
用一个系数$K_d$表示该着色点的光吸收率,范围是$[0,1]$,如果该系数是 0,证明该着色点完全吸收能量,反之,如果是 1,代表该点完全不吸收能量
把这个系数看作是==RGB颜色值==,当$K_d=0$时,此时对应着RGB值是:[0, 0, 0],在计算机里表示为黑色,黑色正是完全吸收光的颜色,反之,当$K_d=1$时,对应着 [255, 255, 255],在计算机里表示为白色,白色正是完全反射光的颜色
最终公式为公式:
$$
L_d=k_d(\frac{I}{r^2})max(0,n·l)
$$
镜面反射
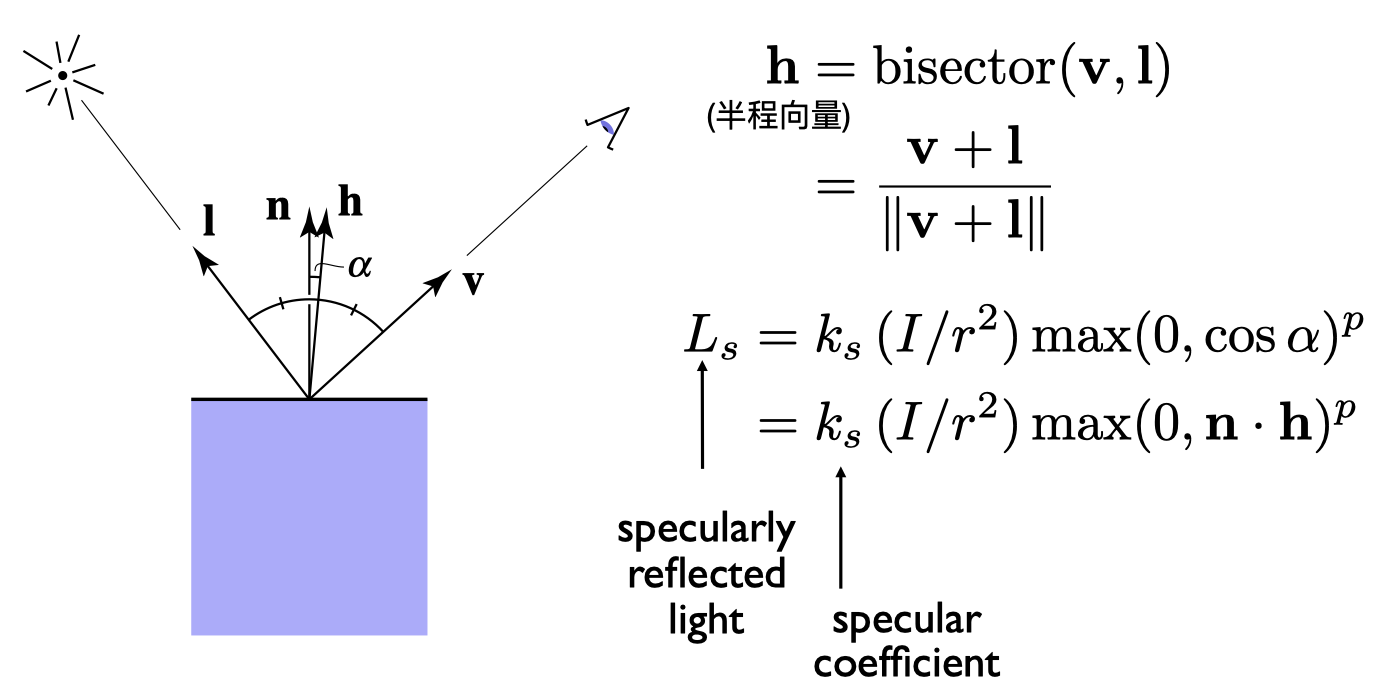
$h$ 为 $l$ 和 $v$ 的半程向量, $n$ 为法线向量, $v$ 为观测角度,
假设前提:观测向量 $v$ 与镜面反射向量 $r$ 的夹角 与 $n$ 和 $h$ 的夹角相等( $R$ 在图中未标明)
why:计算机计算 $v$ 与 $r$ 的角度非常麻烦,考虑到大量像素的性能开销,因此使用较简单的半程向量进行计算
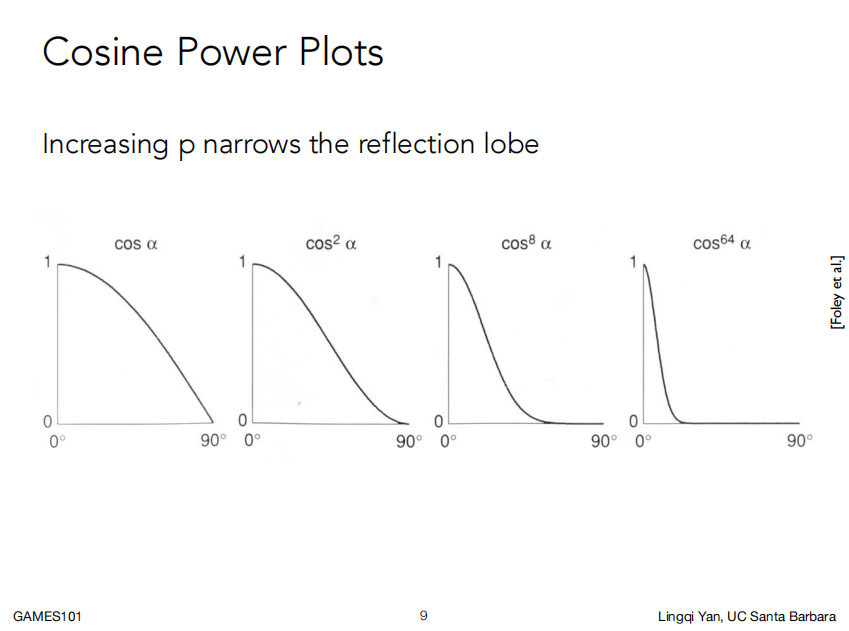 |
 |
|---|
左图:指数p是为了进一步缩小高光范围所提供的的参数,通常取值大于100
右图:不同光照强度和p的取值对高光效果的影响
环境光照
Blinn-Phone光照模型中,假设从四面八方反射而来的光的光强都是相等的,也就是说可以认为环境光强为一个常数(实际上全局光照的计算要复杂的多),公式为$L_a=K_aI_a$
叠加效果
着色频率
Flat Shading(平面着色)
以三角面为单位进行着色,对于光滑的几何体效果很差
Gouraud Shading(高洛德着色)
以顶点为单位进行着色,通过插值计算,实现点与点之间颜色的平滑过渡
Phone Shading(冯氏着色)
以片元为单位进行着色,对每个点计算一次光照,点的法向量是通过顶点法向量插值得到的,冯氏着色最接近现实,可以在减少三角面数的情况下达到相同的效果(插值后法向量会光滑变化),当然,性能开销也非常大
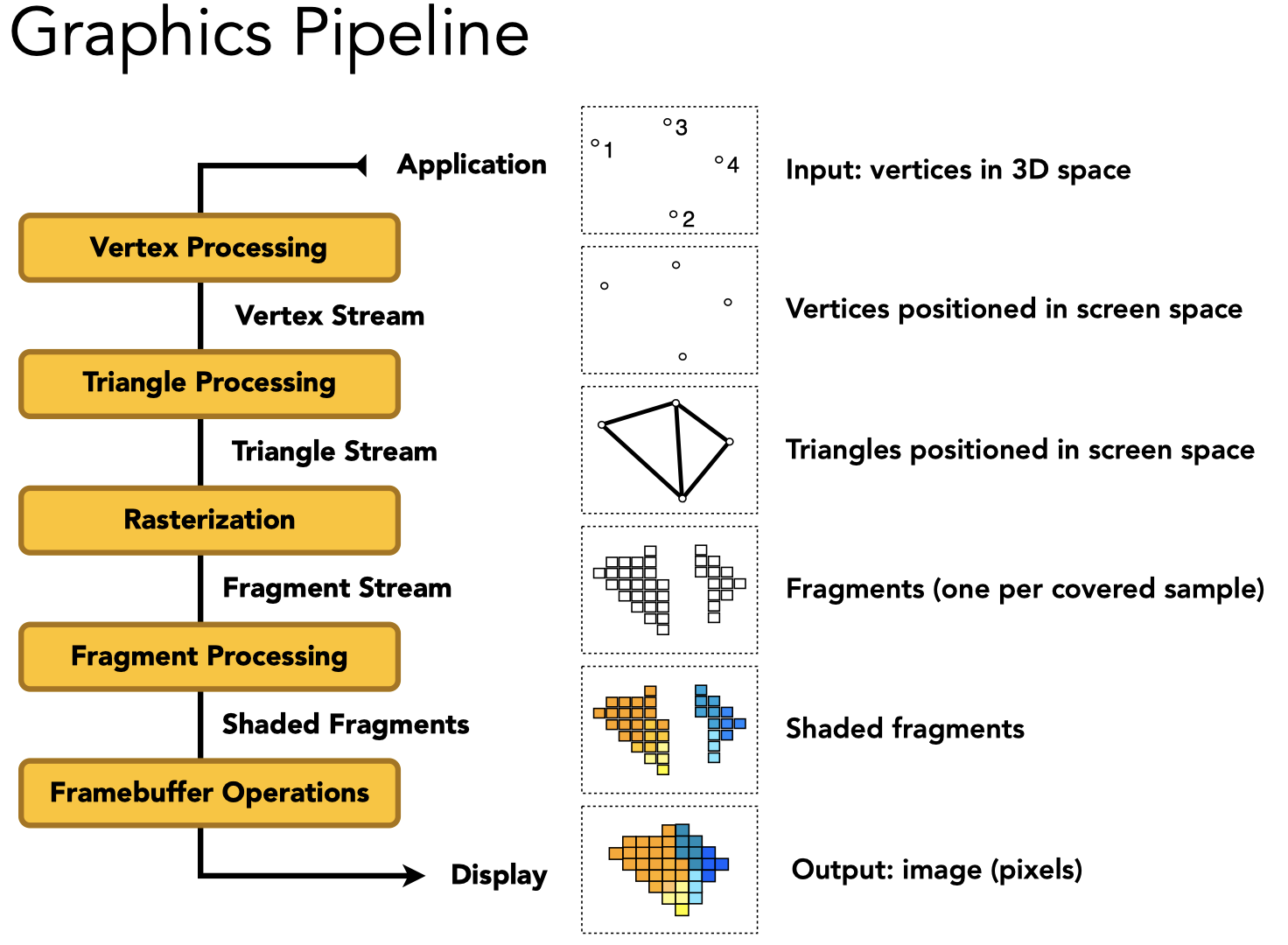
图形管线(实时渲染管线)
顶点处理 -> 三角形处理 -> 光栅化 -> 片元处理 -> 逐片元操作
其中,Vertex和Fragment阶段是可编程的
由于翻译问题,具体可以参考《unity shader入门精要》p9 内容
GPUs:可并行的图形管线处理器
当下的图形实时处理技术可以实时的处理200-400万面的复杂场景数据,并以30-60的帧率动态处理(VR的帧率会更加夸张)
纹理
Texture Mapping 纹理映射
想要在三维物体的不同表面生成不同的纹理,就需要将三维图形的表面映射至二维表面(展UV)
三维图形的每个三角面顶点都可以对应一个uv坐标系下的坐标,uv坐标范围约定在$[0,1]$之间
可复用纹理:纹理本身可以被设计为无缝衔接(tilable),Wang-Tiling是其中一种方法
重心坐标
注意和重心概念的区别!对于三角形所在平面上的任意一点的坐标,都可以用三角形的三个顶点坐标的线性表达式表示
$$
(x,y)=\alpha A+\beta B+\gamma C
$$
则$(\alpha,\beta,\gamma)$被称为该点的重心坐标,定理:$\alpha+\beta+\gamma=1$
对于三角形内的点,$\alpha,\beta,\gamma>0$,更特殊的情况,三角形==重心的重心坐标==为$(\frac{1}{3},\frac{1}{3},\frac{1}{3})$
求$\alpha,\beta,\gamma$公式:
$$
\displaylines{
\begin{aligned}
&\alpha = \frac{-(x-x_B)(y_C-y_B)+(y-y_B)(x_C-x_B)}
{-(x_A-x_B)(y_C-y_B)+(y_A-y_B)(x_C-x_B)}\\
&\beta = \frac{-(x-x_C)(y_A-y_C)+(y-y_C)(x_A-x_C)}
{-(x_B-x_C)(y_A-y_C)+(y_B-y_C)(x_A-x_C)}\\
&\gamma = 1-\alpha -\beta
\end{aligned}
}
$$
推导:
几何意义:$(x,y)$与三角形的三个顶点构成三个三角形,顶点==所对==的三角形的面积与三角形总面积的比值,即为对应的重心坐标值
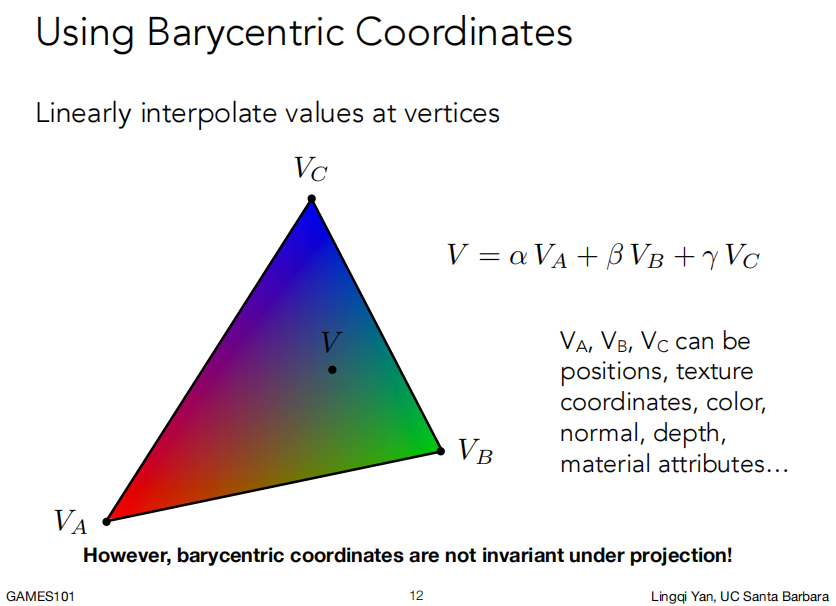
利用重心坐标实现线性插值:
注意,==重心坐标在映射过程中并非保持不变==,所以需要在对应时间计算对应的重心坐标来做插值,不能随意复用!
映射过程伪代码如下:
1 | foreach rasterized screen sample(x,y) //通常来说是一个像素的中心 |
纹理过小 or. 纹理过大?
纹理太小
可以理解为多个pixel映射到了同一个texel
解决方案:
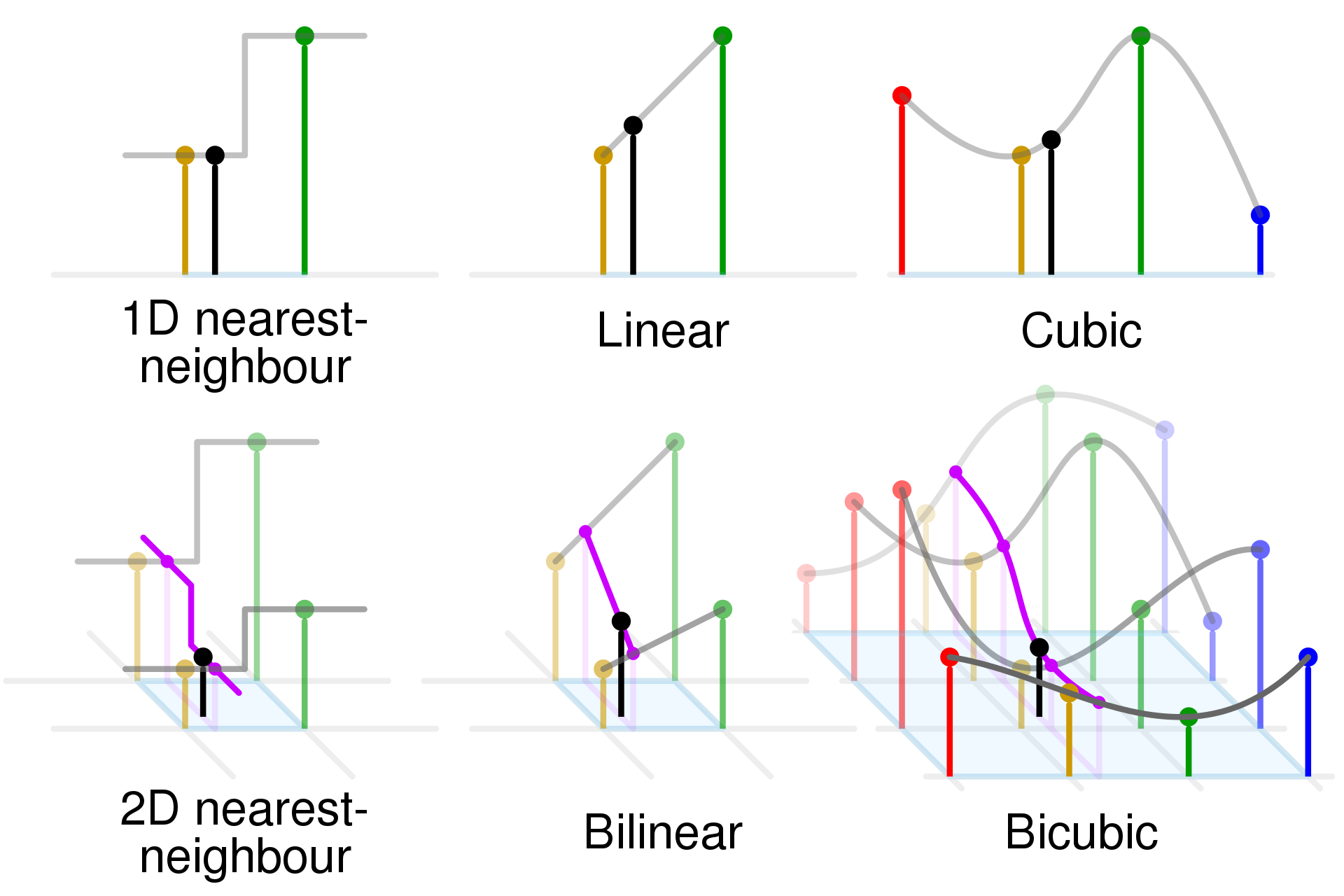
1、水平+竖直做两次插值,即==双线性插值== Lerp
2、对周围16个点做三次插值,==双三次插值== Bicubic,运算量更大,结果更好
纹理太大
可以理解为一个pixel对应了多个纹素,因采样频率不足而导致摩尔纹+锯齿(走样)
解决方案:
Supersampling多重采样,性能开销过大,所以干脆舍弃超级采样的思路
==Mipmap算法:==
事先准备多张不同级别(D)的纹理贴图,每升一个级别,横纵纹素各减小一半,最后显存消耗仅为原来的$\frac{4}{3}$,如此分级之后,设屏幕空间下采样像素与相邻像素中心点之间的距离为L,在u-v坐标系找到这些像素的中心点对应的坐标,求出L在u-v坐标系下对应的纹素数量,做对数运算求得对应像素的纹理细节的级别,再以对应级别做==双线性插值==
由于这种方法中,D是整数,而并非连续的值,为了得到连续的效果,在做对数运算后对小数部分算一下权重,并取向下取整的D值与D+1两个级别,对着两个级别分别做一次双线性插值,最后对插值结果再进行一次插值,我们称这种方法为==三线性插值==
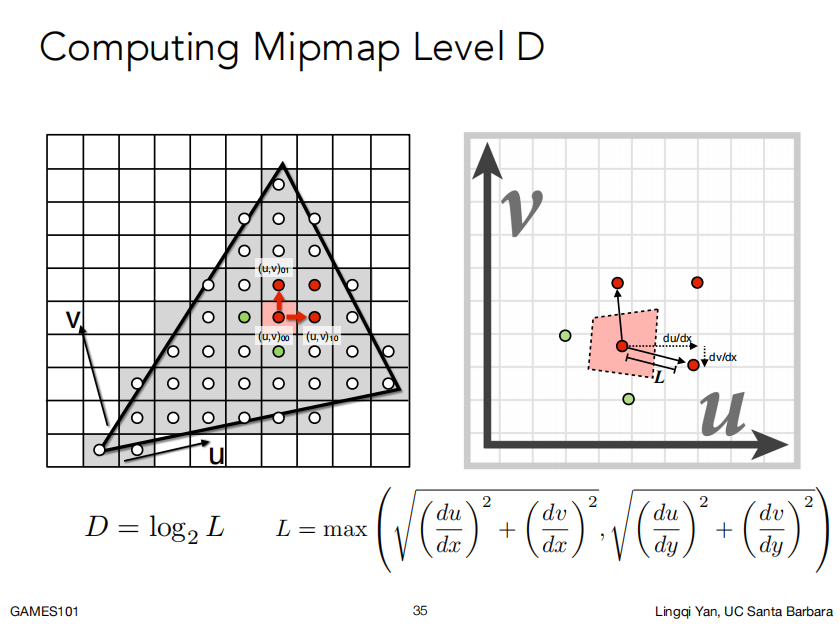 |
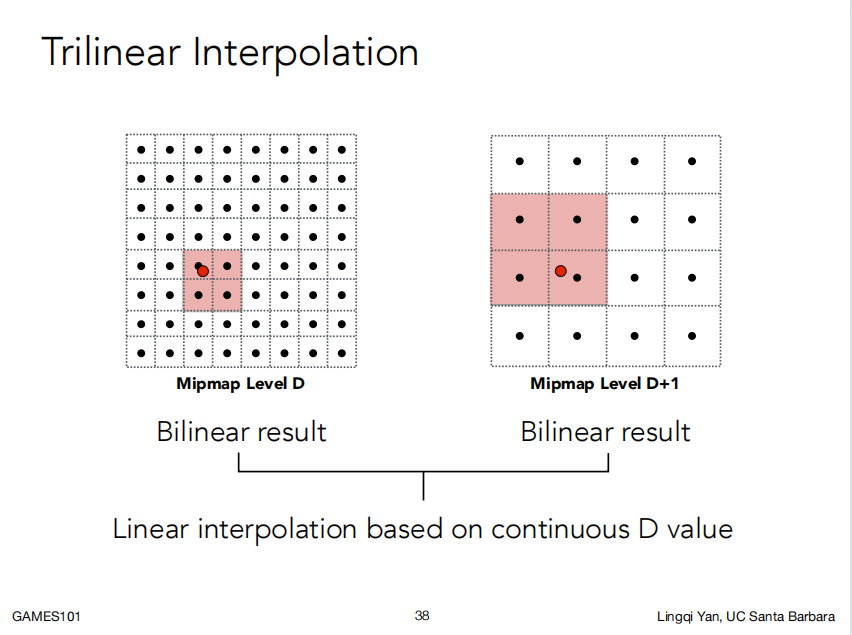 |
|---|
MipMap算法的局限:只能在u-v坐标系下做方块查询,有时候会造成过度模糊的情况
为了避免这种情况,引入==各向异性过滤==,在准备不同级别的纹理贴图时,不再是简简单单横纵纹素各减小一半进行分级,而是长减半宽不变 or 宽减半长不变 or 长和宽各减半三种情况各进行一次分级,显存消耗为原来的三倍,但性能方面并没有多少影响,这种方法就可以实现在u-v坐标系下进行矩形查询。
比各向异性更进一步的过滤,如EWA filtering 椭圆取样,则利用多次查询求平均值的方法来处理不规则区域,相应的性能开销就会比较大了
由上可知,在显存足够的情况下,各向异性过滤级别开越高越好
这块内容显然特别抽象,具体细节可以参考:
各种纹理贴图
环境光贴图
假设光源无限远,只记录光照的方向信息,这种贴图被称作环境光贴图
e.g. Utah Teaport 犹他茶壶;Stanford Bunny 斯坦福兔子
球面环境映射 Spherical Environment Map
球心为世界中心。类比地球仪展开铺平,存在纹理的拉升扭曲问题,解决方法:Cube Map
立方体贴图 Cube Map
将环境光照信息记录在一个立方体表面上,但会需要额外判断某一方向上的光照应该记录在立方体的哪个面上,计算量更大
凹凸贴图
记录了纹理的高度移动,并不改变原来模型的几何信息,通过法线扰动,得到模拟出来的着色效果,以假乱真
计算法线的方法:
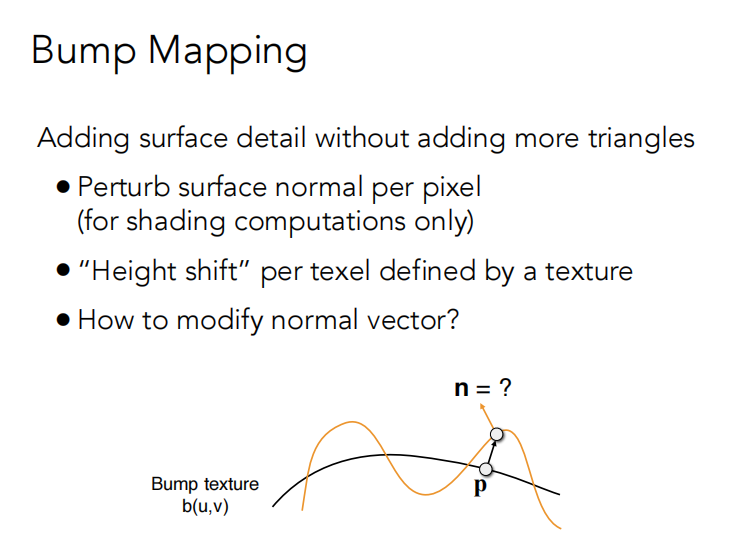 |
 |
|---|
UV下的法线算法:
局部坐标下,$n=\text{normalize}(\text{float3}(-\frac{dp}{du},-\frac{dp}{dv},1))$
置换贴图
与凹凸贴图类似,但置换贴图是真的改变了几何信息,去对模型的顶点做位移,会比凹凸贴图更加逼真,但对模型的精度(三角面数量)要求更高,并且运算量也会随之上升
DirectX有Dynamic的插值法,根据需要对模型做插值,看情况决定模型的细致程度
凹凸贴图vs.置换贴图:
程序纹理
三维的纹理,并非真正生成了纹理的图,而是定义空间中任意点的颜色
定义三维空间中的噪声函数,再通过映射,得到预想的效果
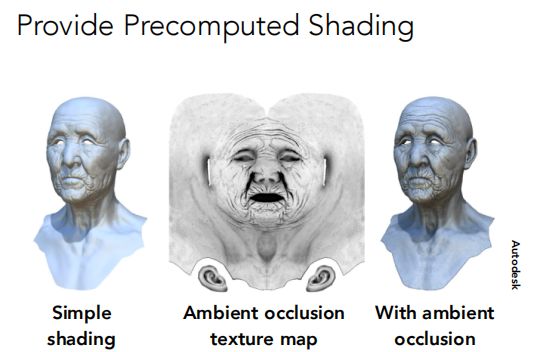
预计算着色
将环境光进行预计算处理,再附在原先纹理上做一层遮蔽(AO),再将纹理贴到模型上
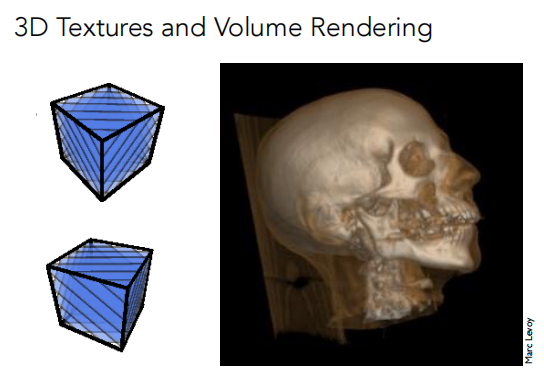
实体建模 / 体渲染
Solid Modeling &. Volume Rendering
广泛应用于物体渲染,如核磁共振等扫描后得到的体积信息,通过这些信息进行渲染,得到结果
| 程序纹理 | 预计算着色 | 实体建模 / 体渲染 |
|---|---|---|
 |
 |
 |






.png)
.png)



